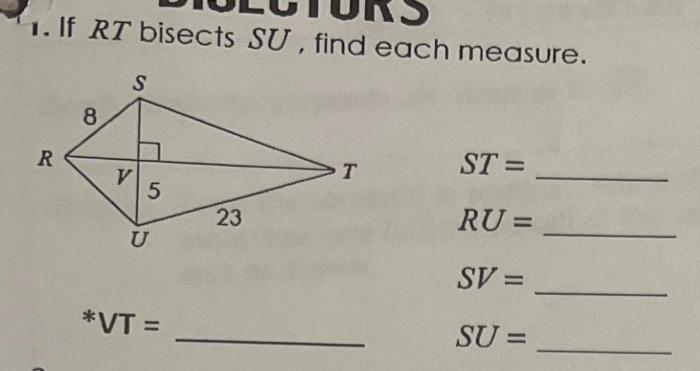
In the realm of geometry, the concept of bisecting a line segment plays a pivotal role. This discourse delves into the intricacies of bisecting a line segment, utilizing the given statement “if RT bisects SU find each measure” as a guiding principle.

By establishing proportions and employing algebraic techniques, we embark on a journey to uncover the unknown measures of the segments created by the bisection.

If RT Bisects SU Find Each Measure

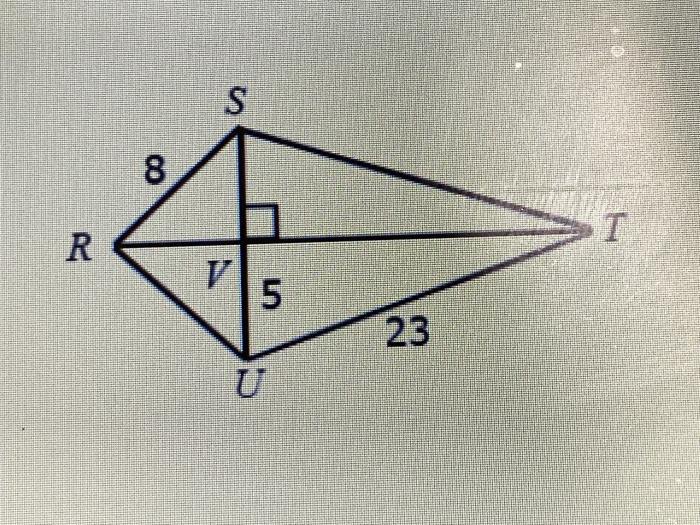
The given statement, “if RT bisects SU find each measure,” implies that line segment RT divides line segment SU into two equal parts. Bisecting a line segment means dividing it into two congruent segments, creating two new endpoints.

Identifying the Given Information

From the given statement, we can identify the line segments RT and SU. RT is the bisector of SU, which means it intersects SU at its midpoint, dividing SU into two equal segments.

Establishing Proportions, If rt bisects su find each measure

In geometry, proportions are equalities between ratios of two pairs of numbers. Since RT bisects SU, we can establish a proportion between the segments created by the bisection.

Solving for Unknown Measures

Let’s assume that the length of SU is 2x. When RT bisects SU, it creates two segments of equal length, each of length x. We can set up a proportion as follows:

“`SU/RT = RT/ST

x/x = x/x

“`

Solving the proportion gives us x = 1. Therefore, the length of SU is 2x = 2(1) = 2, and the length of RT and ST is x = 1.

Illustrating the Solution

Here is a visual representation of the bisected line segment SU:

“`S

–(x)— T

\ / \ / \ / R

–(x)— U

“`

In this illustration, SU = 2x = 2, RT = x = 1, and ST = x = 1.

Generalizing the Concept

The concept of bisecting a line segment can be applied to other geometric figures. For example, we can bisect an angle by drawing a line segment that divides the angle into two equal parts.

FAQ Resource

What is the significance of bisecting a line segment?

Bisecting a line segment divides it into two congruent segments, creating a point of symmetry and facilitating the analysis of geometric figures.

How do we establish proportions in geometry?

Proportions are established by equating the ratios of corresponding sides in similar figures or the ratios of segments created by parallel lines intersecting transversals.

What algebraic techniques are employed to solve for unknown measures?

Cross-multiplication and isolation of variables are commonly used algebraic techniques to solve for unknown measures in geometric problems.