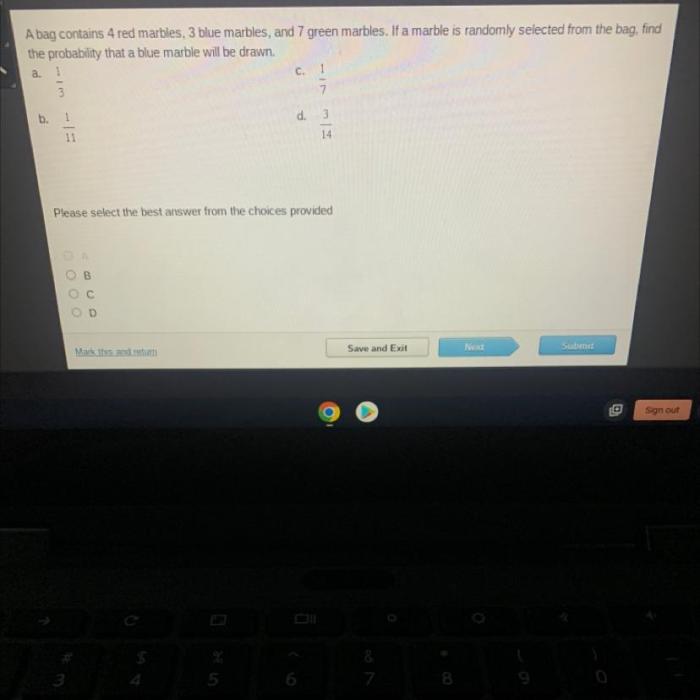
A bag contains 5 red marbles – As the enigmatic bag containing five red marbles takes center stage, this discourse delves into a realm of probability, statistics, and the captivating world of marble distributions. Prepare to embark on an intellectual journey that unravels the mysteries hidden within this seemingly simple object.
The exploration begins with a thorough examination of uniform distribution and the intricacies of drawing a red marble from the bag. We will uncover the formula that governs the probability of selecting a specific color marble from a multicolored collection.
Marble Distribution

In a bag containing multiple marbles, the concept of uniform distribution suggests that each marble has an equal chance of being drawn. This implies that the probability of drawing any particular marble is the same, regardless of its color or any other distinguishing characteristic.
To illustrate, consider a bag containing 5 red marbles and 5 blue marbles. According to the principle of uniform distribution, the probability of drawing a red marble from the bag is 1/10, as each marble has an equal chance of being selected.
Calculating Probability
The probability of drawing a specific color marble from a bag containing multiple colors can be calculated using the following formula:
$$P(A) = n(A) / n(U)$$
Where:
- $P(A)$ is the probability of event $A$ (drawing a specific color marble)
- $n(A)$ is the number of favorable outcomes (marbles of the desired color)
- $n(U)$ is the total number of possible outcomes (all marbles in the bag)
Probability and Combinations
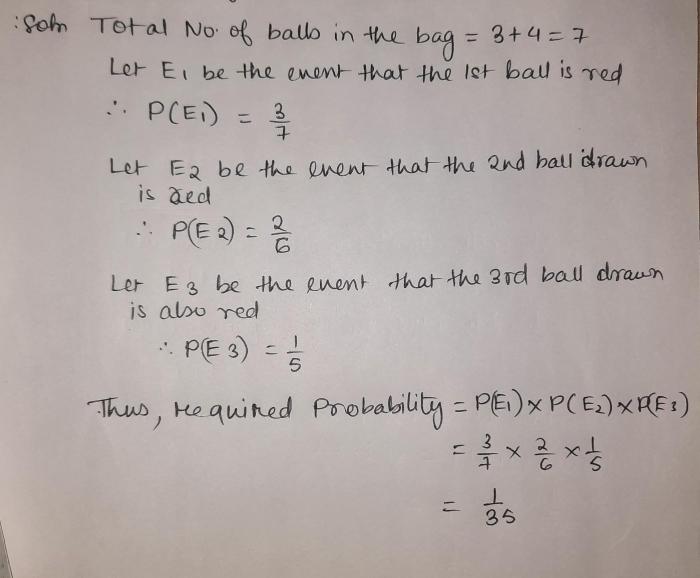
Probability and combinatorics are essential concepts in the analysis of random events, such as drawing marbles from a bag. Understanding these principles is crucial for calculating the likelihood of specific outcomes and making informed decisions.
Fundamental Principles of Probability
Probability measures the likelihood of an event occurring. It is expressed as a number between 0 and 1, where 0 represents an impossible event and 1 represents a certain event. The probability of an event A is denoted as P(A) and can be calculated as:
P(A) = Number of favorable outcomes / Total number of possible outcomes
In the case of drawing marbles from a bag, the favorable outcomes are the specific marbles we are interested in, and the total number of possible outcomes is the total number of marbles in the bag.
Combinations
Combinatorics deals with the number of possible arrangements or combinations of objects. When drawing marbles from a bag, we are concerned with the number of different combinations of marbles that can be drawn. This is important for calculating the probability of specific outcomes.
The number of possible combinations of n objects taken r at a time, denoted as C(n, r), can be calculated using the formula:
C(n, r) = n! / (r!
(n-r)!)
where n! represents the factorial of n, which is the product of all positive integers up to n.
Example
Suppose we have a bag containing 5 red marbles and 3 blue marbles. What is the probability of drawing 2 red marbles without replacement?
First, we need to determine the number of favorable outcomes. There are 5 red marbles, and we need to draw 2. The number of favorable outcomes is C(5, 2) = 10.
Next, we need to determine the total number of possible outcomes. There are 8 marbles in total, and we need to draw 2. The total number of possible outcomes is C(8, 2) = 28.
If a bag contains 5 red marbles, the probability of drawing a red marble is 5 out of the total number of marbles in the bag. This concept is explored in various math tests, including the alice k12 pre test answers . Returning to our bag of marbles, the probability of drawing a red marble remains the same, highlighting the importance of understanding probability concepts.
Finally, we can calculate the probability as:
P(Drawing 2 red marbles) = 10 / 28 = 5 / 14 ≈ 0.357
Therefore, the probability of drawing 2 red marbles without replacement is approximately 0.357 or 35.7%.
Statistical Analysis

Statistical analysis plays a crucial role in understanding the distribution of marbles in a bag. It allows us to determine if the distribution is uniform or if there are any biases or patterns present.
One fundamental concept in statistical analysis is sampling. When we draw marbles from a bag, we are essentially taking a sample from the entire population of marbles. The sample is used to make inferences about the characteristics of the entire population.
Chi-Square Test
The chi-square test is a statistical method used to determine if the distribution of marbles in a bag is uniform. It compares the observed distribution of marbles with the expected distribution under the assumption of uniformity.
Here’s a step-by-step guide to performing a chi-square test:
- Calculate the expected frequency for each category:Divide the total number of marbles by the number of categories (in this case, the number of colors).
- Calculate the chi-square statistic:For each category, subtract the observed frequency from the expected frequency, square the difference, and divide by the expected frequency. Sum the results for all categories.
- Determine the degrees of freedom:Subtract the number of categories from 1.
- Find the critical value:Use a chi-square distribution table to find the critical value for the given degrees of freedom and significance level (usually 0.05).
- Compare the chi-square statistic to the critical value:If the chi-square statistic is greater than the critical value, we reject the null hypothesis and conclude that the distribution is not uniform.
Applications and Extensions

Probability and statistics have numerous applications in real-world scenarios, including the context of drawing marbles from a bag. These concepts help us understand the likelihood of different outcomes and make informed decisions.
One practical application is quality control in manufacturing. By randomly sampling products from a production line and examining their attributes, manufacturers can estimate the overall quality of the entire batch. This helps them identify and address any potential issues, ensuring the consistency and reliability of their products.
Extensions, A bag contains 5 red marbles
The problem of drawing marbles from a bag can be extended in various ways to explore different aspects of probability and statistics.
- Bags with Different Numbers of Marbles:Instead of a bag with 5 red marbles, we can consider bags with different numbers of marbles, such as 10, 20, or 100. This allows us to investigate how the probability of drawing a red marble changes with the size of the bag.
- Bags with Different Colors of Marbles:We can also extend the problem by considering bags with different colors of marbles. For example, we could have a bag with 5 red marbles, 3 blue marbles, and 2 green marbles. This allows us to explore the probability of drawing a specific color of marble and the relationships between different colors.
Simulation
To further analyze the process of drawing marbles from a bag, we can design a simulation to model the process. This involves creating a computer program that randomly selects marbles from a virtual bag and records the results. By running the simulation multiple times, we can gather data on the probability of drawing different colors of marbles and the distribution of outcomes.
User Queries: A Bag Contains 5 Red Marbles
What is the probability of drawing a red marble from the bag?
The probability of drawing a red marble is 5/10, or 1/2.
How many possible combinations of marbles can be drawn from the bag?
There are 252 possible combinations of marbles that can be drawn from the bag.
Can statistical analysis be used to determine if the distribution of marbles in the bag is uniform?
Yes, a chi-square test can be used to determine if the distribution of marbles in the bag is uniform.